Calibration Using LMFIT¶
This example demonstrates the calibration of a simple sinusoidal decay model using the lmfit function. lmfit uses the MINPACK Levenberg-Marquardt algorithm via the lmfit python module.
# %load calibrate_sine_lmfit.py
%matplotlib inline
# Calibration example modified from lmfit webpage
# (http://cars9.uchicago.edu/software/python/lmfit/parameters.html)
import sys,os
try:
import matk
except:
try:
sys.path.append(os.path.join('..','src'))
import matk
except ImportError as err:
print 'Unable to load MATK module: '+str(err)
import numpy as np
from matplotlib import pyplot as plt
# define objective function: returns the array to be minimized
def sine_decay(params, x, data):
""" model decaying sine wave, subtract data"""
amp = params['amp']
shift = params['shift']
omega = params['omega']
decay = params['decay']
model = amp * np.sin(x * omega + shift) * np.exp(-x*x*decay)
obsnames = ['obs'+str(i) for i in range(1,len(data)+1)]
return dict(zip(obsnames,model))
# create data to be fitted
x = np.linspace(0, 15, 301)
np.random.seed(1000)
data = (5. * np.sin(2 * x - 0.1) * np.exp(-x*x*0.025) +
np.random.normal(size=len(x), scale=0.2) )
# Create MATK object
p = matk.matk(model=sine_decay, model_args=(x,data,))
# Create parameters
p.add_par('amp', value=10, min=0.)
p.add_par('decay', value=0.1)
p.add_par('shift', value=0.0, min=-np.pi/2., max=np.pi/2.)
p.add_par('omega', value=3.0)
# Create observation names and set observation values
for i in range(len(data)):
p.add_obs('obs'+str(i+1), value=data[i])
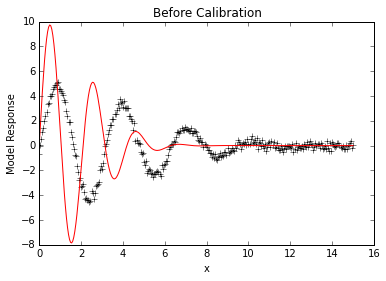
# Look at initial fit
p.forward()
#f, (ax1,ax2) = plt.subplots(2,sharex=True)
plt.plot(x,data, 'k+')
plt.plot(x,p.simvalues, 'r')
plt.ylabel("Model Response")
plt.xlabel("x")
plt.title("Before Calibration")
plt.show()
# Calibrate parameters to data, results are printed to screen
print "Calibration results:"
lm = p.lmfit(cpus=2)
Calibration results:
[[Variables]]
amp: 5.011399 +/- 0.040469 (0.81%) initial = 5.011398
decay: 0.024835 +/- 0.000465 (1.87%) initial = 0.024835
omega: 1.999116 +/- 0.003345 (0.17%) initial = 1.999116
shift: -0.106184 +/- 0.016466 (15.51%) initial = -0.106207
[[Correlations]] (unreported correlations are < 0.100)
C(omega, shift) = -0.785
C(amp, decay) = 0.584
C(amp, shift) = -0.117
None
SSR: 12.8161378922
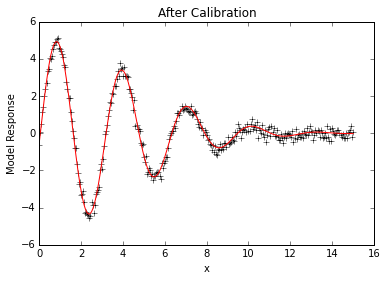
# Look at calibrated fit
plt.plot(x,data, 'k+')
plt.plot(x,p.simvalues, 'r')
plt.ylabel("Model Response")
plt.xlabel("x")
plt.title("After Calibration")
plt.show()